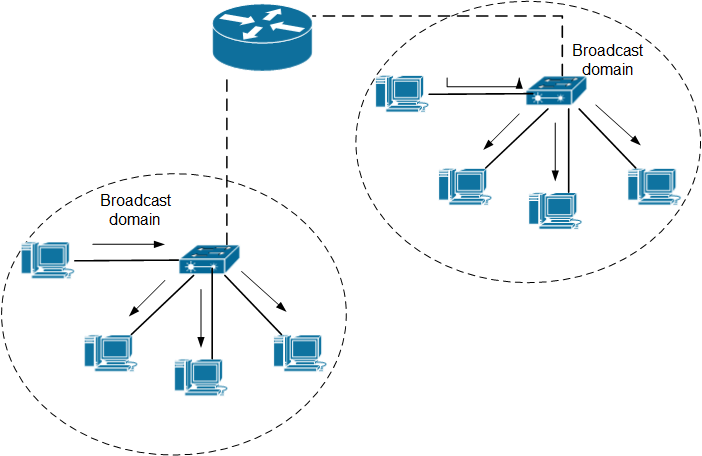
A broadcast domain is a logical division of a computer network, in which all nodes can reach each other by broadcast at the data link layer. A broadcast domain can be within the same LAN segment or it can be bridged to other LAN segments.
In terms of current popular technologies: Any computer connected to the same Ethernet repeater or switch is a member of the same broadcast domain. Further, any computer connected to the same set of inter-connected switches/repeaters is a member of the same broadcast domain. Routers and other higher-layer devices form boundaries between broadcast domains.
This is as compared to a collision domain, which would be all nodes on the same set inter-connected repeaters, divided by switches and learning bridges. Collision domains are generally smaller than, and contained within, broadcast domains.
While some layer two network devices are able to divide the collision domains, broadcast domains are only divided by layer 3 network devices such as routers or layer 3 switches. Separating VLANs divides broadcast domains as well, but provides no means to network these without layer 3 functionality.
Further explanation
The distinction between broadcast and collision domains comes about because simple Ethernet and similar systems use a shared transmission system. In simple Ethernet (without switches or bridges), data frames are transmitted to all other nodes on a network. Each receiving node checks the destination address of each frame, and simply ignores any frame not addressed to its own MAC.
Switches act as buffers, receiving and analyzing the frames from each connected network segment. Frames destined for nodes connected to the originating segment are not forwarded by the switch. Frames destined for a specific node on a different segment are sent only to that segment. Only broadcast frames are forwarded to all other segments. This reduces unnecessary traffic and collisions.
In such a switched network, transmitted frames may not be received by all other reachable nodes. Nominally, only broadcast frames will be received by all other nodes. Collisions are localized to the network segment they occur on. Thus, the broadcast domain is the entire inter-connected layer two network, and the segments connected to each switch/bridge port are each a collision domain.
Not all network systems or media feature broadcast/collision domains. For example, PPP links.
Broadcast domain control
With a sufficiently sophisticated switch, it is possible to create a network in which the normal notion of a broadcast domain is strictly controlled. One implementation of this concept is termed a "private VLAN". Another implementation is possible with Linux and iptables. One helpful analogy is that by creating multiple VLANs, the number of broadcast domains increases, but the size of each broadcast domain decreases. This is because a virtual LAN (or VLAN) is technically a broadcast domain.
This is achieved by designating one or more "server" or "provider" nodes, either by MAC address or switch port. Broadcast frames are allowed to originate from these sources, and are sent to all other nodes. Broadcast frames from all other sources are directed only to the server/provider nodes. Traffic from other sources not destined to the server/provider nodes ("peer-to-peer" traffic) is blocked.
The result is a network based on a nominally shared transmission system; like Ethernet, but in which "client" nodes cannot communicate with each other, only with the server/provider. A common application is Internet providers. Allowing direct data link layer communication between customer nodes exposes the network to various security attacks, such as ARP spoofing. Controlling the broadcast domain in this fashion provides many of the advantages of a point-to-point network, using commodity broadcast-based hardware.