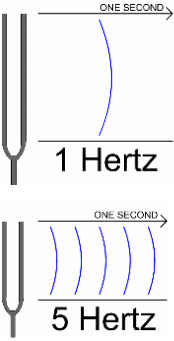
The hertz (symbol Hz) is the unit of frequency in the International System of Units (SI) and is defined as one cycle per second. It is named for Heinrich Rudolf Hertz, the first person to provide conclusive proof of the existence of electromagnetic waves.
One of the unit's most common uses is in the description of sine waves and musical tones, particularly those used in radio and other audio-related applications. It is also used to describe the speeds at which computers and other electronics are driven.
Definition
The hertz is equivalent to cycles per second. In defining the second, the International Committee for Weights and Measures declared that "the standard to be employed is the transition between the hyperfine levels F = 4, M = 0 and F = 3, M = 0 of the ground state 2S1/2 of the cesium 133 atom, unperturbed by external fields, and that the frequency of this transition is assigned the value 9 192 631 770 hertz" thereby effectively defining the hertz and the second simultaneously.
In English, "hertz" is also used as the plural form. As an SI unit, Hz can be prefixed; commonly used multiples are kHz (kilohertz, 103 Hz), MHz (megahertz, 106 Hz), GHz (gigahertz, 109 Hz) and THz (terahertz, 1012 Hz). One hertz simply means "one cycle per second" (typically that which is being counted is a complete cycle); 100 Hz means "one hundred cycles per second", and so on. The unit may be applied to any periodic event—for example, a clock might be said to tick at 1 Hz, or a human heart might be said to beat at 1.2 Hz. The rate of aperiodic or stochastic events occur is expressed in reciprocal second or inverse second (1/s or s?1) in general or, the specific case of radioactive decay, becquerels. Whereas 1 Hz is 1 cycle per second, 1 Bq is 1 aperiodic radionuclide event per second.
Even though angular velocity, angular frequency and the unit hertz all have the dimension 1/s, angular velocity and angular frequency are not expressed in hertz, but rather in an appropriate angular unit such as radians per second. Thus a disc rotating at 60 revolutions per minute (rpm) is said to be rotating at either 2? rad/s or 1 Hz, where the former measures the angular velocity and the latter reflects the number of complete revolutions per second. The conversion between a frequency f measured in hertz and an angular velocity ? measured in radians per second is
and .
This SI unit is named after Heinrich Hertz. As with every International System of Units (SI) unit named for a person, the first letter of its symbol is upper case (Hz). However, when an SI unit is spelled out in English, it should always begin with a lower case letter (hertz)—except in a situation where any word in that position would be capitalized, such as at the beginning of a sentence or in material using title case. Note that "degree Celsius" conforms to this rule because the "d" is lowercase.— Based on The International System of Units, section 5.2.
History
The hertz is named after the German physicist Heinrich Hertz (1857–1894), who made important scientific contributions to the study of electromagnetism. The name was established by the International Electrotechnical Commission (IEC) in 1930. It was adopted by the General Conference on Weights and Measures (CGPM) (Conférence générale des poids et mesures) in 1960, replacing the previous name for the unit, cycles per second (cps), along with its related multiples, primarily kilocycles per second (kc/s) and megacycles per second (Mc/s), and occasionally kilomegacycles per second (kMc/s). The term cycles per second was largely replaced by hertz by the 1970s.
Applications
Vibration
Sound is a traveling longitudinal wave which is an oscillation of pressure. Humans perceive frequency of sound waves as pitch. Each musical note corresponds to a particular frequency which can be measured in hertz. An infant's ear is able to perceive frequencies ranging from 20 Hz to 20,000 Hz; the average adult human can hear sounds between 20 Hz and 16,000 Hz. The range of ultrasound, high-intensity infrasound and other physical vibrations such as molecular vibrations extends into the megahertz range and well beyond.
Electromagnetic radiation
Electromagnetic radiation is often described by its frequency—the number of oscillations of the perpendicular electric and magnetic fields per second—expressed in hertz.
Radio frequency radiation is usually measured in kilohertz (kHz), megahertz (MHz), or gigahertz (GHz). Light is electromagnetic radiation that is even higher in frequency, and has frequencies in the range of tens (infrared) to thousands (ultraviolet) of terahertz. Electromagnetic radiation with frequencies in the low terahertz range, (intermediate between those of the highest normally usable radio frequencies and long-wave infrared light), is often called terahertz radiation. Even higher frequencies exist, such as that of gamma rays, which can be measured in exahertz. (For historical reasons, the frequencies of light and higher frequency electromagnetic radiation are more commonly specified in terms of their wavelengths or photon energies: for a more detailed treatment of this and the above frequency ranges, see electromagnetic spectrum.)
Computers
For more details on why the frequency, including for gigahertz (GHz) etc., is a flawed speed indicator for computers, see Megahertz myth.
In computers, most central processing units (CPU) are labeled in terms of their clock rate expressed in megahertz or gigahertz (106 or 109 hertz, respectively). This number refers to the frequency of the CPU's master clock signal ("clock rate"). This signal is a square wave, which is an electrical voltage that switches between low and high values at regular intervals. Hertz has become the primary unit of measurement accepted by the general populace to determine the performance of a CPU, but many experts have criticized this approach, which they claim is an easily manipulable benchmark as some processors use multiple clock periods to perform a single operation, while others can perform multiple operations in a single cycle. For home-based personal computers, CPU clock speeds have ranged from approximately 1 MHz in the late 1970s (Atari, Commodore, Apple computers) to up to 6 GHz in IBM POWER processors.
Various computer buses, such as the front-side bus connecting the CPU and northbridge, also operate at various frequencies in the megahertz range.
The "speed" or the more correct term bandwidth of networks, including wireless, such as Wi-Fi, 3G, 4G, LTE, etc. is not affected by the myth described above. In general, higher frequency means higher bandwidth or bit rates, that lower the times to download big files. In general, however, higher frequencies do not pass through walls, making lower frequencies an advantage e.g. indoors (most common equipment reports the highest frequency used, but usually also work at lower, making this often not a problem). Bandwidth is often equated with "speed", while latency ("lag"), is the perceived problem, that is a distinct measure from bandwidth, while higher bandwidth has an influence on latency.
SI multiples
SI multiples for hertz (Hz)
| Submultiples | Multiples | ||||
|---|---|---|---|---|---|
| Value | SI symbol | Name | Value | SI symbol | Name |
| 10?1 Hz | dHz | decihertz | 101 Hz | daHz | decahertz |
| 10?2 Hz | cHz | centihertz | 102 Hz | hHz | hectohertz |
| 10?3 Hz | mHz | millihertz | 103 Hz | kHz | kilohertz |
| 10?6 Hz | µHz | microhertz | 106 Hz | MHz | megahertz |
| 10?9 Hz | nHz | nanohertz | 109 Hz | GHz | gigahertz |
| 10?12 Hz | pHz | picohertz | 1012 Hz | THz | terahertz |
| 10?15 Hz | fHz | femtohertz | 1015 Hz | PHz | petahertz |
| 10?18 Hz | aHz | attohertz | 1018 Hz | EHz | exahertz |
| 10?21 Hz | zHz | zeptohertz | 1021 Hz | ZHz | zettahertz |
| 10?24 Hz | yHz | yoctohertz | 1024 Hz | YHz | yottahertz |
| Common prefixed units are in bold face. |
Higher frequencies than the International System of Units provides prefixes for, are believed to occur naturally in the frequencies of the quantum-mechanical vibrations of high-energy, or, equivalently, massive particles, although these are not directly observable and must be inferred from their interactions with other phenomena. For practical reasons, these are typically not expressed in hertz, but in terms of the equivalent quantum energy, which is proportional to the frequency by the factor of Planck's constant.